In this research, a new framework is proposed to improve supply chain management in CBEC, combining optimization techniques and machine learning for sales volume prediction of factors, and using fuzzy logic and auction theory to allocate resources to sellers. This section presents the suggested design after detailing the data structure that was employed in the study.
Data
The research data was collected over a two-year period through the sales records of 10 active sellers in the CBEC domain. All sales factors are supported through a common supplier, and each seller utilizes multiple online sales platforms for marketing and selling their products. The collected data in this research describes the weekly sales volume for each seller and includes only records of physical product sales. The number of online sales platforms used by each seller ranges from 3 to 7, and some factors use shared platforms for product sales. The data used in the current study consists of 110 records for each seller, describing the total sales volume in the last seven days (across all platforms used) as a natural number within the range of 44 to 185. In addition to sales volume, each data record includes a set of features appears in Table 1.
Proposed framework
In the proposed framework for optimizing supply chain management in the CBEC system, it involves a set of retail sellers, each utilizing multiple online sales platforms for marketing and selling their products. Each retail seller has a warehouse to store their resources, which is supported by a common supplier. In traditional supply chain models, online customers place orders through the desired product sales platforms, and the retail seller fulfills the customer’s order using their warehouse inventory. When the inventory of a product decreases or runs out, the retail seller will request support from the common supplier. This reactive process in supply chain management can lead to decreased efficiency in the CBEC sales system because delayed product supply by the supplier can result in customer dissatisfaction and attrition.
On the other hand, maintaining excess product inventory in the retail sellers’ warehouses can lead to resource wastage in the supply chain. Additionally, supplying a common product (with limited inventory) among multiple retail sellers needs to align with each seller’s performance. These characteristics make it necessary for the supply chain system to have an active strategy for fulfilling the demands effectively.
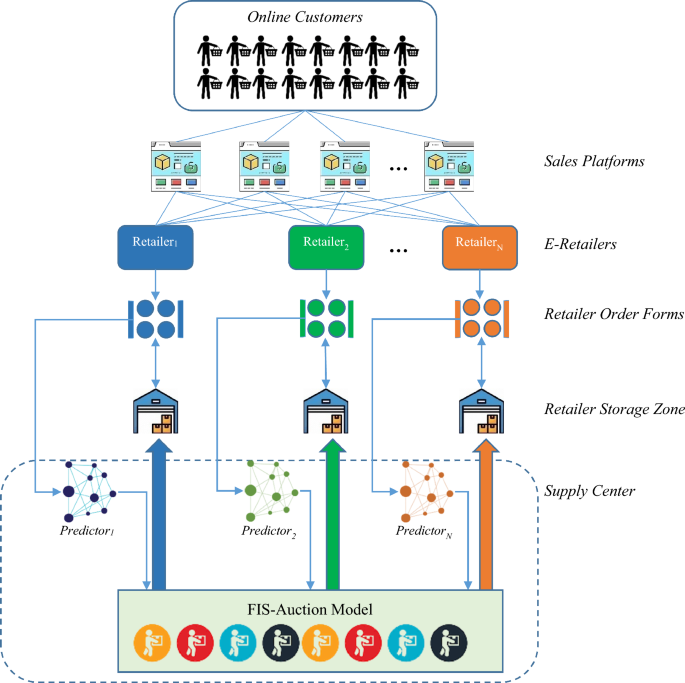
In this paper, a combined strategy for optimizing supply chain performance in CBEC is presented, which fairly distributes limited supplier resources among retail sellers while considering the forecasted needs of the retail sellers. The mechanism of the proposed strategy is depicted in Fig. 1.

Proposed Framework for Supply Chain Performance Optimization.
Figure 1 demonstrates, the proposed method focuses on intelligent resource allocation for retail sellers in a CBEC system. The suggested framework is made up of three primary parts:
-
A prediction model to estimate the future orders of each retail seller.
-
A fuzzy model for evaluating each seller’s resource requirements.
-
An auction model for the fair distribution of resources among retail sellers.
In this approach, the future needs of each retail seller are predicted using a custom neural network-based learning model. This learning model, trained based on the sales history of the respective seller, utilizes a black-hole optimization algorithm to adjust its weight vector. The prediction values obtained from this neural network are then used to determine the seller’s resource requirements through a fuzzy model.
After executing the above processes for all retail sellers, the value of each seller in terms of resource allocation is estimated using an auction model. Ultimately, the resource allocation pattern is determined based on the values assigned by this auction model. The proposed resource allocation model for retail sellers’ mechanism is depicted in a diagram in Fig. 2.

Determining the Resource Allocation Pattern among Retailers in the Proposed Methodology.
As shown in Fig. 2, the proposed model, after selecting relevant indicators for the order volume of each retail seller, uses a separate ANN (Artificial Neural Network) for predicting the future order volume for that seller. This ANN model utilizes a black-hole optimization algorithm to determine its weight and bias vector, aiming to find a combination of weight values that minimizes the training error. Using an independent ANN model for each retail seller allows for a more precise modeling of each seller’s transaction patterns. This approach can better identify functional differences among sellers in terms of marketing and sales in different time periods.
The predicted values from the ANN model, along with the current inventory and current sales features, are used as inputs to a fuzzy model to estimate the retail seller’s resource renewal needs for the next period as a fuzzy variable. In Fig. 2, the details of these processes for retail seller i are depicted.
The processes of predicting future sales and assessing the resource renewal needs for each retail seller are repeated, and the results from these processes are used as inputs to an auction model. This auction model describes the value of each seller for resource allocation as a numerical value. Finally, by normalizing these values, the resource allocation pattern among retail sellers is determined.
The continuation of this section provides a detailed explanation of each of the above-mentioned stages.
Sales volume prediction based on ANN and BHO
The first step in the proposed method involves predicting the future sales volume of retail sellers using optimization and machine learning techniques. Accurate sales volume prediction can help estimate the resource needs of sellers for future periods and manage the supply chain accordingly. Since each seller has a different performance pattern, and their sales volume is directly related to their marketing activities, it’s not feasible to use a shared model for predicting the sales of all sellers. For this reason, in the proposed method, each retail seller utilizes a separate learning model to predict their sales volume, which is trained solely based on features related to their performance history.
However, to achieve an efficient prediction model, two fundamental issues need to be addressed. Firstly, sales volume prediction should be based on indicators related to the seller’s performance pattern. For example, for a seller who intensifies their marketing activities during specific time intervals, time-based indicators are more important compared to sellers whose marketing activities are consistent over time. The second issue is the necessity of using an optimized configuration for the learning model to ensure the minimum prediction error. The proposed model tackles the first issue using a feature selection strategy based on ANOVA and FSFS (Feature Selection via Feature Space). To address the second requirement, the model uses the BHO (Black-Hole Optimization) algorithm to fine-tune the ANN model. Consequently, the sales volume prediction process in the proposed method consists of two detailed steps, which are discussed further in this section.
(A) Feature Selection Before training the ANN model based on features related to the performance history of the retail seller, a feature selection algorithm is used to determine the most relevant factors with the sales pattern. Removing irrelevant factors can not only increase the processing speed of the model but also have an impact on reducing its error while reducing the model’s dependence on multiple data points. These advantages make the feature selection process highly important for achieving an efficient prediction model. The suggested technique does this by combining the FSFS algorithm and ANOVA.
In this process, each data record is first described as follows:
$${Y}^{t+1}:\langle {I}_{1}^{t},{I}_{2}^{t},\dots ,{I}_{19}^{t}\rangle$$
(1)
where I_k^t represents the k-th feature describing the performance of the retail seller in a time period (week) t, which is extracted based on Table 1. Additionally, Y^(t + 1) represents the sales volume in the next week (t + 1), which can be extracted from the next data record related to sales data.
In the feature selection algorithm used, all candidate factors (Eq. 1) are first ranked using one-sided ANOVA analysis to assess the importance of each factor using the F-statistic. The F-value in one-sided variance analysis represents the ratio of between-group variation to within-group variation, where higher F-values indicate that the data between groups is more diverse compared to within groups. This property can indicate the presence of a meaningful and different pattern for identifying data groups.
Existing features are rated in descending order according to their F-statistic values in order to choose relevant features for the proposed technique. Then, the SFS (Sequential Forward Selection) algorithm is used to identify the right amount of features. In this procedure, the target variable (future sales) is estimated using an artificial neural network-based estimating model based on various combinations of rated features. In this instance, the target variable is estimated using the two features that had the greatest rankings, and the training error is assessed. Then, the next feature is added to the selected feature set, and the training error is evaluated again. If the training error decreases compared to the previous iteration, the added feature is retained; otherwise, the feature is removed from the selected feature set, and the process ends.
Finally, a combination of ranked features that results in the lowest training error is considered as the selected feature set. It’s important to note that the feature selection process is carried out separately for each retail seller.
(b) Sales Volume Forecasting.
After determining the most relevant indices, the process of predicting future sales volume based on these indices is carried out. If we represent the selected set of indices by S = {I_(s(1))^t, I_(s(2))^t, …, I_(s(n))^t}, then the prediction process can be formulated as follows:”
$${Y}^{t+1}=f\left(S\right)=f({I}_{s(1)}^{t},{I}_{s(2)}^{t},\dots ,{I}_{s(n)}^{t})$$
(2)
In the above equation, “f” displays a function that models the relationship between performance factors at time “t” and the sales volume at time “t + 1”. An ANN (Artificial Neural Network) model is employed in this step of the suggested methodology to estimate this relationship. Within the proposed approach, the sales volume prediction model for each retailer is created using an Artificial Neural Network.
The BHO (Black Hole Optimization) approach is used to modify the neural network’s weight vector as opposed to more conventional training procedures. The goal of this optimization procedure is to establish the neural network’s weight vector based on the training error (which serves as its own fitness function). Figure 3 depicts the structure of the neural network utilized in the suggested technique for forecasting each retailer’s sales volume.

The Structure of the Neural Network Used in the Proposed Retailer Sales Volume Forecasting Method.
In Fig. 3, the neural network structure used in the proposed method for predicting the sales volume of each retailer is depicted. The neural network consists of an input layer, two hidden layers, and an output layer. The input layer is fed with the selected features from the previous step. The first and second hidden layers contain 18 and 10 neurons, respectively, with sigmoid logarithmic and linear activation functions assigned to these two layers. Finally, the output layer comprises a single neuron that represents the predicted sales volume for the input sample.
As mentioned, the BHO (Black Hole Optimization) algorithm is used for training this neural network. In the following sections, the structure of the response vector and the fitness function for convergence evaluation will be explained, followed by the steps of training the ANN model using BHO.
The neural network’s biases and the weights of connections between neurons are determined by the response vector in the BHO algorithm, which is employed in the proposed method. The BHO algorithm’s response vector length for a neural network with I input neurons, H1 neurons in the first hidden layer, H2 neurons in the second hidden layer, and P output neurons will be equal to:
$$L={H}_{1}\times \left(I+1\right)+{H}_{2}\times \left({H}_{1}+1\right)+P\times ({H}_{2}+1)$$
(3)
In the equation above, H1 × (I + 1) represents the number of weight values between the input layer and the first hidden layer plus the bias of the first hidden layer. H2 × (H1 + 1) indicates the number of weights between the first and second hidden layers plus the bias of the second hidden layer. Finally, P × (H2 + 1) signifies the number of weights between the last two layers plus the bias of the output layer. Thus, the length of each solution vector in BHO will be L. In this vector, the weight and bias values are described as real numbers within the range [-1, + 1]. In other words, each optimization variable in BHO is represented as a real variable with search bounds [-1, + 1].
Using a fitness function, the BHO algorithm assesses the fitness of each solution. The outputs of the neural network are generated for the training samples and contrasted with the actual goal values once each response vector’s weights have been determined. The effectiveness of the neural network and the calibre of the response generated are then assessed using the mean squared error (MSE). As a result, the following definition will serve as the fitness function for the BHO algorithm:
$$MSE=\frac{1}{N}\sum_{i=1}^{N}{\left({y}_{i}-{t}_{i}\right)}^{2}$$
(4)
In the equation above, N stands for the quantity of training samples, ti for the i-th training sample’s goal value, and yi for the neural network’s output for the i-th training sample. In the suggested approach, a neural network topology that can reduce the fitness function is chosen using an optimisation technique.
It’s important to note that the BHO algorithm randomly generates the initial population.
Step 1 Make a random initial population of solution vectors in step 1.
Step 2 Apply Eq. (4) to get the fitness for each solution vector.
Step 3 Define the black hole (X_BH) as the solution with the lowest fitness.
Step 4 Reposition each answer (star) so that it is similar to X_i as follows:
$${X}_{i}={X}_{i}+rand.({X}_{BH}-{X}_{i})$$
(5)
In Eq. (5), X_i denotes the location of star/solution i in the problem space, while X_BH denotes the location of the black hole. The term “rand” refers to a random number between 0 and 1.
Step 5 Perform the following calculation to determine the distance at which a star can be sucked up by a black hole:
$$R=\frac{fitness(BH)}{\sum_{i=1}^{N}fitness(i)}$$
(6)
N here refers to the quantity of solution vectors used in the BHO algorithm.
Step 6 Replace the existing black hole with a solution vector if its fitness is lower than the black hole’s.
Step 7 Substitute a new random solution vector for any solution vectors that are closer to the black hole than the threshold R.
Step 8 Continue to the next step if the number of algorithm iterations surpasses the threshold T; else, start over at step 2 with the search.
Step 9 Present the black hole with the lowest fitness as the most effective solution that has been found.
The ANN model produced by using this solution vector will be employed by the store for sales volume forecasting in subsequent time intervals when the best solution has been determined based on the aforementioned processes.
Evaluating each retailer’s resource requirements using fuzzy logic
The suggested technique’s second step, a fuzzy logic model is used to assess the resource requirements of each retailer. Using fuzzy logic for this task allows modeling decision-making under uncertainty, which increases the flexibility of the model for decision-making in the next step. This fuzzy logic model evaluates the resource needs of each retailer based on their current information and predicted status. The structure of this fuzzy model is depicted in Fig. 4.

Proposed Fuzzy Model for Assessing the Retailer’s Resource Renewal Level.
The fuzzy model utilised in Fig. 4 is the Mamdani fuzzy inference system, which contains 18 fuzzy rules, one output variable, and three input variables. The membership functions for the input and output variables in this fuzzy system are shown in Fig. 5.

Membership Functions of Fuzzy Variables in the Proposed Method.
In Fig. 5a, the membership functions of the predicted sales volume, which is essentially the value predicted by the neural network in the previous step, are displayed. Figures b and c show the membership functions for the current sales volume and inventory level, respectively, which are the input variables. Finally, the output fuzzy variable with 5 membership functions is presented in Figure d. In the following, I will explain how each of these variables is calculated.
The expected sales volume for the forthcoming period is the first input of this fuzzy system and is determined by the proposed neural network and described by three membership functions: “low,” “medium,” and “high.” This input variable’s normalization for the suggested fuzzy model is as follows:
$${I}_{1}=\frac{Sale{s}_{predict}}{\underset{j}{\text{max}}Sale{s}_{j}}$$
(7)
In the above equation, Sales_predict represents the predicted sales volume by the proposed ANN model, and Sales represents the vector of historical sales volume for the current retailer. The retailer’s current inventory level is defined by the second fuzzy input variable, which has the membership functions “low” and “high,” and is described by the following equation:
$${I}_{2}=1-\frac{Sale{s}_{current}}{Inv}$$
(8)
In the above equation, Inv represents the current inventory level of resources in the dedicated store for the current retailer, and Sales_current represents the current sales volume in the backlog. Finally, the third fuzzy input variable in the proposed fuzzy inference system is the current product sales volume, which is described by three membership functions: “low,” “medium,” and “high,” and is calculated using the following equation:
$${I}_{3}=\frac{Sale{s}_{current}}{\underset{j}{\text{max}}Sale{s}_{j}}$$
(9)
The output of the fuzzy system will use the stated fuzzy variables to determine the degree to which a retailer needs resource replenishment from the supplier. In the proposed fuzzy model, this output variable is determined using the rules provided in Table 2.
After prioritizing the determination of each retailer’s resource replenishment needs by the supplier, all the calculated results for the retailers are used as inputs to the proposed auction model. Ultimately, the resource allocation to each retailer is carried out through this model.
Equitable distribution of resources among small retailers based on auction theory
In the third phase of the proposed method, the allocation of resources to retailers is based on auction theory. Given the predictions of future sales volume and the assessed resource replenishment needs of each retailer, the goal is to distribute resources fairly while maximizing the overall profitability of the CBEC model, considering the constraints of the supplier’s resources.
The theory of auctions, a branch of applied economics, focuses on how individuals behave in auction markets and analyzes the characteristics of auction markets. Over time, various auction mechanisms, efficiency, desirable pricing strategies, optimization, equilibrium of bidding strategies, and income comparisons have been studied extensively by theorists for auctions and related topics. Auctions are transactions where, based on participants’ bids, a particular set of rules and resource allocations are determined. Auctions are classified as incomplete information games because, in most cases, one party does not have complete information about the other party’s deal. For example, participants usually know their own valuation of the product, but this valuation is unknown to other participants and sellers. Auctions come in various forms, but a common feature among them is their universality, as they can be used for the purchase or sale of various items. These characteristics make auction theory a suitable choice for addressing the research problem in this study.
There are many categories for different types of auctions in this theory. For example, auctions can be one-dimensional or multi-dimensional, they can be one-sided or two-sided, bids can be open or sealed, and the items can be single-unit or multiple-unit, and so on. In the proposed method, a sealed-bid auction model with a first-price mechanism is used to determine the resource allocation pattern among the retailers by the supplier. In the proposed method, a sealed-bid auction model with a first-price mechanism is used to determine the resource allocation pattern among the retailers by the supplier. In this auction model, buyers submit their sealed bids simultaneously to the sellers. These bids are observed by the sellers, and the most acceptable price will be chosen. In this auction model, no one will be able to see the rival’s bid before submitting their ownIn the proposed model, the retailers in need of resources are considered as buyers in the sealed-bid auction model, and the common supplier in the supply chain is considered as the seller of this model. The item being traded, in reality, represents the resources to meet the needs of the retailers. In this case, the price is also described as a function of the current status and the future status of the seller.
In the proposed auction model, a time period, such as “s,” is considered, representing the time interval that covers the resource provisioning for the retailers. In each execution of the proposed auction model, the supplier offers resources to the buyers for the time period “s.” Participants in the auction include the set of previously unsuccessful retailers from the previous auction and the new retailers in need of resources.
The goal of the proposed auction model is to distribute “m” products belonging to the supplier among “n” products needed by the retailers. If “n” is greater than “m,” at least one retailer will fail in the auction process and will need to participate in the next auction to secure the required resources. In the proposed method, the proposed price for each retailer in the auction model is calculated as follows:
$$P=F\times \frac{Sale{s}_{current}+Sale{s}_{predict}-Inventory}{{\text{log}}_{2}(N)}$$
(10)
In the above equation:
-
\(Sale{s}_{current}\) represents the current sales volume awaiting order completion.
-
\(Sale{s}_{predict}\) describes the predicted sales volume for the time period s + 1 by the ANN model.
-
Inventory characterizes the current inventory of the retailer.
-
N shows how many times the retailer has been unsuccessful throughout the bidding process.
-
F represents the priority value determined by the proposed fuzzy model.
To distribute resources based on the above equation, initially, the supplier removes all retailers with negative proposed prices. The eliminated retailers are considered as unsuccessful buyers in the current auction. For this set of unsuccessful retailers, the value of N for each of them is increased by one to improve their chances of success in the next auction. Then, the remaining set of proposed prices (positive prices) is normalized using the following formula.
$$P_{i} = \frac{{P_{i} }}{{\mathop \sum \nolimits_{j = 1}^{R} P_{j} }}$$
(11)
In the equation above:
-
Pi represents the proposed price by retailer i, which is calculated using Eq. (10).
-
R denotes the number of successful retailers in the current auction.
Finally, the allocated share for each retailer is determined using the provided formula.
$${Z}_{i}={P}_{i}\times m$$
(12)
In the equation above, m represents the number of resources available for allocation to all the retailers in the current auction by the supplier.