EVATOM: an optical, label-free, machine learning assisted embryo health assessment tool

Embryo culture and staining procedure

Animals

Sexually mature B6D2F1 males and CD1 females at 35–42 days old were purchased from Charles River Laboratories (Wilmington, MA). The mice were housed at the Carl R. Woese Institute for Genomic Biology at the University of Illinois, Urbana-Champaign. All the mice were provided with feed and water ad-libitum and housed in individually ventilated cages under a controlled environment. Animal rooms were maintained at 22 ± 1 °C with a 12-h light cycle. B6D2F1 males were housed individually for breeding setup purposes. Animal handling and procedures were performed in accordance with the University of Illinois Institutional Animal Care and Use Committee (protocol number: 23004). We have complied with all relevant ethical regulations for animal use.

Chemicals

Ovarian superovulation was achieved using pregnant mare serum gonadotropin (PMSG, Cat. Nor-272-a, Prospec, East Brunswick, NJ), and human chorionic gonadotropin (HCG, Cat. C1063-1VL, MilliporeSigma, Burlington, MA). Materials for in-vitro culture, including potassium simplex optimized medium (KSOM, Cat. MR-121-D) and hyaluronidase, were purchased from MilliporeSigma (Burlington, MA) and sterile mineral oil (Cat. ART-4008-5P) from CooperSurgical (Trumbull, CT). OMOPS handling medium consisted of MgSO4 (1.2 mM); Glucose (0.5 mM); L-Lactate (6.0 mM); GlutaGRO (1.0 mM); Tarine (0.1 mM); NEAA (1x); EDTA (0.01 mM); Alpha Lipoic Acid (10 uM); Gentamicin (10 ug/ml); Hyaluronan (0.125 mg/mL); NaHCO3 (5.0 mM); MOPS (20.0 mM); pyruvate (0.2 mM); Citrate (0.5 mM); FAF BSA (4.0 mg/ml). A pure phthalate mixture was made by calculating and combining the appropriate amount of each phthalate according to the following percentages 35% DEP, 21% DEHP, 15% DBP, 15% DiNP, 8% DiBP, and 5% BBzP in 0.05% DMSO. Phthalates were purchased from Sigma. In previous, preliminary studies, incubation of mouse embryos in this phthalate mixture, at 1 µg/mL, reduced blastocyst formation by 50%. This concentration was used to produce the sick batch of embryos.

Embryo collection and in vitro culture

To induce superovulation, 35 to 42 days old female mice were injected intraperitoneally with 6 IU of PMSG, followed by 6 IU of HCG 48 h post PMSG. Injections were performed at 2:00 to 3:00 pm. After the HCG injection, female mice were housed individually with male mice overnight. The following day, at approximately 20 h post-hCG, the female mice were inspected for a copulation plug and euthanized by CO₂ inhalation and cervical dislocation. Oviducts were collected aseptically and placed in a pre-warmed OMOPS medium supplemented with 5% fetal bovine serum (FBS, Atlanta Biologicals) and were maintained at 37 °C during collection and transportation. Embryos were released from the oviducts into the OMOPS medium using forceps to gently tear open the ampulla. The embryos were rinsed a minimum of three times with OMOPS medium before being introduced into a droplet of OMOPS medium containing hyaluronic acid (500 µg/ml) for cumulus cell removal. Exposure to hyaluronic acid was limited to a maximum of one minute. The embryos were rinsed two more times in clean OMOPS droplets until cumulus cells were removed. Cumulus-free embryos were placed into pre-equilibrated KSOM droplets under mineral oil. All the embryos were cultured in a ThermoFisher 8000 WJ CO₂ incubator at 37 °C, 6% CO₂, and 80% relative humidity until the mid-morning of day 5, 116 ± 2 h post-HCG injection, at which point they were either fixed or imaged live for assessment using an Olympus IX70 phase contrast microscope.

Fixation of embryos and immunofluorescence staining for 7-AAD

The embryos were fixed in freshly prepared 50:50 methanol:acetone at 1:1 volume ratio at −20 °C for 20 min. They were then transferred to Holding Medium (50 ml PBS + 0.25 g BSA (0.5%)), droplets covered with mineral oil, and maintained at 4 °C until staining.

Immunofluorescence staining for 7-Aminoactinomcyin D (7-AAD) was carried out as follows: fixed embryos were placed in permeabilization buffer (50 ml PBS + 500 µl Triton X-100 (1%)) for one hour. Embryos were then washed three times for 10 minutes in Washing Buffer (500 ml PBS + 500 µl Triton X-100 (0.1%) + 0.5 g poly-vinyl-pyrrolidone (0.1%)). Embryos were then incubated with the 7-AAD Red Fluorescent Live/Dead Stain from Immunochemistry Technologies (#6163) at a 1:200 dilution for 30 min in the dark at room temperature followed by three 10-minute washes in Washing Buffer. Finally, embryos were mounted in 3 mm glass bottom dishes with 14 mm micro-well in 20 µL of mounting medium containing DAPI for 30 min in the dark at room temperature. Embryo droplets were covered with 100 µL of mineral oil, coverslipped and kept in the dark at 4 °C for 24–48 h before imaging.

Image acquisition and reconstruction

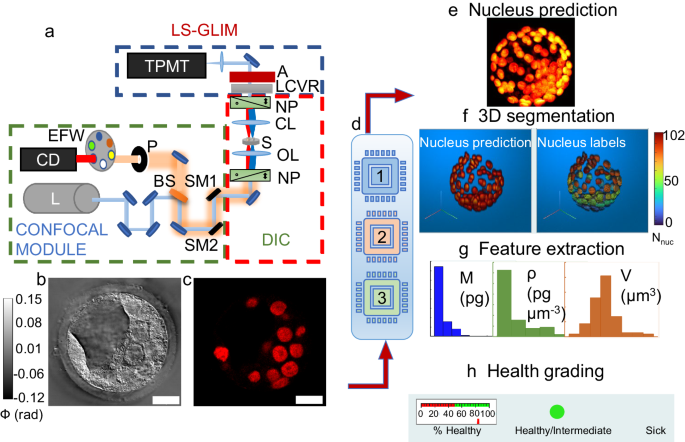
Embryos were imaged using a laser-scanning GLIM setup with confocal fluorescence detection for nucleus ground truth data²⁷. A standard Zeiss Axio Observer microscope was equipped with an Airyscan LSM 900 module for fluorescence confocal operation and a GLIM module for quantitative phase detection for the same field of view. The system has two laser sources with wavelengths of 488 nm, and 561 nm. The microscope was operated using Zeiss Zen software for setting the experiment parameters, and the image acquisition was controlled by a custom build MATLAB code developed by Chen et al.²⁷. However, we modified the acquisition code for automated stage movement, coordinate tracking, and tomographic acquisition for multiple fields of view. All images were obtained using a Plan-Apochromat 40x/1.3 Oil DIC (UV) VIS-IR M27 objective with the pinhole set to 1.09 AU. The wavelength of the laser source for LS-GLIM was 488 nm, operated at 1% power with a detector gain of 350 and digital gain of 1. Four intensity images corresponding to phase shifts of \(n\pi /2\), for n = 0,1,2,3, were recorded at the transmission photomultiplier tube (T-PMT). From the 4-intensity images, a phase gradient image was extracted using the phase-shifting interferometric reconstruction algorithm as detailed in Nguyen et al.²⁵. The final phase image was obtained after applying Hilbert transform-based integration to the phase gradient image²⁵.

Phase images convey information about the sample’s composition in terms of dry mass and dry mass density¹⁵ because of the linear relationship between dry mass density and phase. The relation between dry mass and phase can be expressed as¹⁵:

where, M is the dry mass, \(\lambda\) is the illumination wavelength, \(\gamma\) is the refractive index increment, and \(\varphi ({{{{{\bf{r}}}}}})\) is the measured 3D phase. The dry mass density is then evaluated as the average dry mass over the volume (V) of the sample.

For fluorescence detection of the 7-AAD nucleus signal (peak excitation and emission at 549/648 nm), excitation at 561 nm with 2% laser power, detector gain 750-800, and digital gain 1 were used.

The scan mode was set to frame for each channel, and pixel dwell time was 1.21 µs. In addition, the laser scan speed was set to 6 in a bidirectional scan mode. Tomographic acquisition of each embryo was done with a step size of 1 µm in the z-direction.

For the live embryo imaging, the microscope incubator (a sealed structure) was maintained at 37 °C and supplied with 6% CO₂ to maintain medium pH and match the culture conditions used prior to imaging. The imaging environment was humidified to avoid evaporation / changes to medium composition during the imaging procedure.

Nucleus prediction model architecture and training details

The nucleus prediction model (NPM) is a UNet-style model with an Efficient Net-B0 encoder^42,43,44. The architecture is shown in Supplementary Fig. 1a with the submodule information in Supplementary Fig. 1b. We first trained the model on a pair of images from LS-GLIM with corresponding images of the fluorescence-stained nuclei (Supplementary Fig. 14a and Supplementary Fig. 14b, respectively, from an unseen test dataset with prediction in Supplementary Fig. 14c). The input image and the target image size were 1280 ×1280 pixels each. An example input image is shown in Supplementary Fig. 14d. The fluorescence target image (Supplementary Fig. 14e) was median filtered with a window size of 5 to reduce spurious pixel noise (Supplementary Fig. 14f). The predictions (Supplementary Fig. 14c) also contain spurious background detections in the cell cytoplasm area because of the presence of a weak background signal in the fluorescence ground truth itself, more evident in Supplementary Figs. 14b, c middle row (white arrows). To remove this background noise and increase the specificity of detection a preprocessing step was added for the target image. The histograms of the denoised fluorescence image were matched with the corresponding LS-GLIM image using the MATLAB function “imhistmatch”. The overall effect of this step was similar to thresholding, where negative pixels in the LS-GLIM (that mostly correspond to the background/cytoplasm) were zeroed out in the target fluorescence image. Another effect was that the target fluorescence image was much more specific now, such that slightly defocused nuclei and cytoplasmic signals were removed, as evident in Supplementary Fig. 14g. With the training set now containing images like Supplementary Fig. 14d as input and Supplementary Fig. 14g as the target, the model was able to remove spurious detections, as shown in Supplementary Fig. 14h. Images from the test set showing the predictions of both the models is shown in Supplementary Figs. 14i-l, where Supplementary Fig. 14i is the input GLIM image, Supplementary Fig. 14j is the corresponding denoised target fluorescence image, Supplementary Fig. 14k is the first model prediction (without histogram matching), where the spurious cytoplasmic signals are also present (as indicated by white arrows) and Supplementary Fig. 14l shows the final model prediction (trained on a histogram-matched target), where the increased specificity is evident. The numerical results of both model comparisons are shown below each prediction. The final model shows an increased PSNR and MS-SSIM. The Pearson correlation coefficient (PCC) decreased after histogram matching. The visual results indicate the superiority of our final model. Thus, PCC was not found to be a good metric for this task.

The model was trained on a combination loss which is a linear combination of L1 loss, MS-SSIM loss, and Pearson loss defined as:

where, l, c, and s, are the luminance, contrast, and structure comparison measures as defined elsewhere⁶¹. MS-SSIM definition is followed from Ref. ⁶¹

The final loss is

The weights of the loss components were determined empirically to be [2,1,0.5] for L1, MS-SSIM, and Pearson loss, respectively. Our choice of the loss function was inspired by a previous study⁶², where the authors have demonstrated the superiority of the L1 and MS-SSIM loss combination. The Pearson loss was used to overcome the image artifacts observed in previous studies (unpublished).

A mixed strategy¹⁹ of learning-rate warmup and cosine decay was followed for the learning rate, increasing it from 0 to the specified 1e-4 in the first 6 epochs and later decreased following cosine learning decay. From the loss curve (Supplementary Fig. 1c), training was stopped after the 10^th epoch because no further improvement in validation loss was observed after the 8^th epoch. The low number of epochs is justified because of the large dataset employed for the training. Specifically, 4265, 1280 ×1280 pixels sized images were used for training that increased in number to 8530 training instances after augmentation. An additional 1434 images were used as the validation set, and a hold-out test set containing 1407 images was used for final testing. In total, 96 embryos were used: 55 for training, 20 for validation, and 21 for testing of the model. The Adam optimizer was used for loss optimization. Test metrics on the unseen hold-out dataset are shown in Supplementary Fig. 1d with PSNR 36.94, MS-SSIM 0.94, and PCC 0.81, respectively.

The model framework was based on a library⁶³ in Tensorflow 2.3. We trained the model on NVIDIA GeForce RTX 2080 Ti. The training for 10 epochs took 4 hours and 56 minutes.

Health grading data annotation

Embryos were cultured in culture medium only (untreated), or culture medium containing pure phthalate mixture (treated) to halt growth and mimic a population of poor quality/developmentally arrested embryos. After imaging, z-composite LS-GLIM images (maximum phase projection) of the z-stack were computed for each embryo in the whole sample set to pass on to the embryologists for annotation. We observed a range of embryo development and the differences in the development were taken into consideration while grading the embryos. Embryo grading was performed using standard morphological assessment criteria adopted by clinical laboratories; blastocoel existence and expansion, quality (lack of granular appearance, evident cell fragmentation, number, and arrangement of the TE and ICM). One of the three grades: healthy, intermediate, or sick, was assigned to each embryo by one or more expert embryologists. Untreated embryos could therefore fall into any of the three categories. However, treated embryos would be graded as intermediate or sick depending on the severity of damage induced by the treatment. The intermediate label was subjective in that the embryo’s fate was unknown at the time of fixation. The data collected over several rounds of sample preparation and imaging experiments were combined into one collective dataset with a total of 152 embryos graded as 46 healthy, 65 intermediate, and 41 sick. The training, validation, and initial test data were then extracted from this collective dataset individually for each health grading model (see below). An additional test dataset of 43 embryos was subsequently merged with the initial test dataset giving a total of 195 embryos used for model development.

3D segmentation and feature extraction

3D nuclei predictions were stacked up into a volume, and the 3D nuclei features were extracted using a 2-step segmentation procedure. The first step of the segmentation involved 2D segmentation per z-section image. Each z-section image of size 1280 ×1280 pixels was median filtered with a window size of 19 pixels in both dimensions to make the intensity uniform and then normalized between its minimum and maximum value. The images were then hard thresholded using a threshold of 0.2, removing any stray detections in the non-nuclei area. Following the hard-thresholding, adaptive thresholding with a sensitivity of 0.55 and a window size of 145 pixels in each dimension was performed to generate a nuclear binary mask. Morphological operations such as opening and area filtering with a cut-off of 400 pixels² (corresponding to a radius of ~ 1 µm) were performed to correct for non-specific detections after binarization. Next, a watershed algorithm was applied to separate nuclei whose borders were touching. After the watershed, other rounds of area filtering were applied to remove elements below the size cut-off of 60 pixels in diameter (~5 µm), with solidity below 0.8, to remove over-segmented artifacts. The cut-offs of area and solidity were derived empirically after observing the minimum size of nuclei in the images and the associated solidity of the binary mask over the nuclei. Each nucleus in a z-section image of an embryo was assigned a unique label. The exact process was repeated for all z-section images of the entire embryo. The next task was to connect these 2D labels to form 3D labels. Centroids of each nucleus were tracked in the z-direction, and nuclei in two adjacent z-section images were assigned to the same trajectory if their Euclidean distance between the centroids was within a specified sensitivity (50 pixels radius in xy plane). This cut-off was chosen because the two smallest nuclei adjacent to one another would have at least 60 pixels of the distance between their centroids. After assigning centroids to trajectories, we checked for breaks in the trajectory for the cases of nuclei stacked on one another along the z-dimension. To find such separator boundaries, we looked for a series of local minima in the z-direction for the area of the 2D slice of the nuclei and the distance from the first centroid in the trajectory. Gaps in trajectories of more than 5 µm were used as the definition of a new nuclear boundary. Each nucleus in a 3D trajectory was assigned one unique label and was added to the existing embryo 3D label volume. Finally, filtering based on empirically determined minimum volume in voxels (5000 px³), maximum volume (250000 px³), minimum z-depth (3), and minimum extent (0.14) of the 3D nuclear volume was performed to remove over/under-segmented particles. After 3D segmentation, each nucleus in an embryo volume was assigned a unique color-coded identification label that corresponds to the identity of individual nucleus (Fig. 2f). It is important to note that this 3D segmentation remains in the pixels domain, and rendering at this point will not accurately represent the 3D volume. For proper 3D measurements, the labeled volume was resized by the lateral pixel ratios (11 pixels per µm) and z-step size (1 µm), and the labels are interpolated along the z-direction using ‘nearest’ interpolation such that an accurate 3D representation is achieved, while maintaining the labels across the interpolated volume. The phase volume was interpolated with linear interpolation in the z-axis.

The max value projection of the labeled image can then be used for producing a nuclear count map, as shown in Supplementary Fig. 4, with the color bar denoting the number of nuclei in a single embryo. Features representing nuclear shape descriptors (volume, surface area, sphericity) and nuclear composition descriptors (dry mass and dry mass density) were then extracted for each nucleus. Embryo-level features (nucleus count, scattering amplitude spectrum bandwidth) based on the aggregate system of nuclei inside an embryo were also extracted after 3D segmentation. For subsequent data analysis, nuclei with sphericity greater than 1 were excluded as those represented under-segmented clusters.

We also prepared a normalized dry mass density map per embryo (Fig. 4 and Supplementary Fig. 6) based on the extracted nuclear dry mass density. The color of each nucleus represents the mean nuclear dry mass density averaged over its volume. The volume was Gaussian filtered with standard deviations of (1,1,3) for x, y, and z dimensions respectively to enhance the smoothness of the 3D representation. Each embryo was then normalized over the volume for meaningful comparisons between different embryos.

Scattering amplitude modeling

The distribution of nuclei inside an embryo can be modeled as a system composed of multiple identical repeating units. The scattering potential of such a system can be expressed as¹⁵

The contribution of individual repeating units is represented by the delta functions placed at different position vectors \({{{{{{\bf{r}}}}}}}_{{{{{{\bf{n}}}}}}}\), * denotes 3D convolution in the spatial domain and \({F}_{0}({{{{{\bf{r}}}}}})\) is the scattering potential of a single unit.

The scattering amplitude¹⁵ can then be expressed as the Fourier transform of Eq. (6)

where, q is the scattering wave vector with \(|q|=2{k}_{0}\,\sin \theta /2\), \(\theta\) is the scattering angle and \({k}_{0}\) is the free-space propagation constant.

The two terms of this equation convey different information. The first term \({F}_{0}({{{{{\bf{q}}}}}})\) is the form function, which represents the scattering amplitude’s envelope, while the fluctuations within the envelope are determined by the second term \(S({{{{{\bf{q}}}}}})=\mathop{\sum}\limits_{n}{e}^{i{{{{{{\bf{r}}}}}}}_{{{{{{\bf{n}}}}}}}\cdot {{{{{\bf{q}}}}}}}\), and defined as the structure-function. The form function is the Fourier transform of the scattering potential of a single repeating unit and is dependent on the shape of that unit. The structure function is the aggregate effect of all repeating units and is only affected by the distribution of such units inside the system’s volume. For an embryo the repeating units are represented by the individual nuclei. To make the assumption of identical repeating units valid, nuclei were replaced with a unit sphere centered at the centroid of each nucleus. In doing so, the size/shape variability between the nuclei was eliminated. Since we used nuclei predictions to construct the 3D embryo space, we do not have any other part of the embryo, like cell cytoplasm, etc., in our system. The resultant modeled embryo systems for a healthy/intermediate and a sick embryo are shown in Supplementary Fig. 3a, b respectively. The modeled system’s 3D Fourier transform (a product of form and structure functions) can then determine differences in the embryos based on their health class. A maximum intensity projection along the \({{{{{{\bf{k}}}}}}}_{{{{{{\bf{z}}}}}}}\) direction of the scattering amplitude spectrums for the corresponding healthy/intermediate and sick embryos are different (Supplementary Fig. 3c, d respectively), indicating a difference in power distribution. It is important to note that the maximum projection is only shown for visualization purposes, and all the calculations are performed in the 3D spatial frequency domain. The raw radial average of the power spectral density of scattering amplitude is shown in Supplementary Fig. 3e for all 152 embryos, where the red curves are associated with sick embryos, the blue curve for intermediate embryos, and the green curve for healthy embryos. It is immediately observed that the curves for healthy and intermediate embryos overlap. To illustrate the difference between the three classes, the curves were averaged per group (Supplementary Fig. 3f) and divided by their respective peak powers to get the final normalized radially averaged powers spectral density of the scattering amplitudes for the three classes (Supplementary Fig. 3g).

To calculate the bandwidths of the scattering amplitude spectrum per embryo, images were downsized in the xy plane to prepare a 3D volume and enable a 256-point FFT in each spatial direction. The frequency space was also rescaled accordingly to get the correct spatial frequencies. After placing unit radii spheres at the centroids of individual nuclei, we performed a 3D FFT to calculate the spectrum. The spatial frequency \(|{{{{{\bf{k}}}}}}|=\sqrt{({k}_{x}^{2}+{k}_{y}^{2}+{k}_{z}^{2})}\) was discretized into 256 levels, and a radial average of the spectrum was calculated on a thin spherical shell covered between successive elements of the k vector.

The 3 dB or 50% power bandwidth was extracted from the radial average, representing the bandwidth at which the power drops to 50% of its peak power and was used as an essential feature in health grading.

Health grading of embryos

Based on our analysis of parameters between the healthy, intermediate, and sick embryos, we found that there are insignificant differences between the parameters of healthy and intermediate embryos, while highly significant differences between either healthy and intermediate versus sick embryos (Supplementary Table 1). This information was used to group the embryos into two classes: a combined H/I class (healthy and intermediate embryos) and S class (sick embryos). Our task was to classify each embryos’ health into these two classes-H/I or S. To test the accuracy of health classification based on the extracted features only, we trained a neural network classifier. We called this model a feature-based model (FBM) for health grading. In addition, to take advantage of the state-of-the-art models, we trained a second deep learning model that would not require any hand-engineered features as it will predict the health of the embryos from the LS-GLIM images alone. We called this second model an image-based model (IBM) for embryo health grading.

FBM architecture and training details

The features used for training were those showing higher statistical significance and only one feature is selected from the feature pairs with a correlation above 0.6 (for example dry mass-dry mass density and volume-surface area) on the heatmap in Supplementary Fig. 2h. Nucleus count (nuc_count) displayed a high negative correlation (~−0.7) with scattering amplitude spectral bandwidth (bw3dB), however it was included in the feature vector because it represents the absolute number of nuclei per embryo (Supplementary Fig. 4). The selected features were arranged in a tabular dataset with five predictors: bw3dB, nucleus count, nuclear dry mass density, nuclear surface area, nuclear sphericity, and two responses 0 (for H/I) or 1 (for S). Data from the 152 embryos were divided such that 102 embryos were used for training, 16 for validation, 34 were kept as holdout data for testing to be combined with another experimental dataset of 43 embryos for full testing. The initial model type search was performed in MATLAB Classification Learner app with the model type selection set to all models. The models were tested on the combined test dataset as well as on the live test dataset (19 instances of live embryos). For the final common test dataset comparing both the models (FBM and IBM), 5 embryos from the combined test set were not included because they had been used in the validation set of the IBM. The combined test and live performance of neural network classifiers exceed other classifier models (Supplementary Table 4). A neural network-based classifier architecture was therefore selected and optimized to improve the results further.

The FBM is a feedforward, fully connected 3-layer neural network with hidden layers of size [10, 2], constructed and trained using fitcnet in MATLAB, with the architecture as shown in Supplementary Fig. 15a. The hidden layer activations were ReLU and the output activation was SoftMax. Model weights were initialized with Glorot initialization with the biases initialized to zeros. The early stopping is controlled by validation patience, gradient tolerance, and loss tolerance which are set to 20, 1e−9, and 1e−9, respectively. The loss function is the standard cross-entropy loss with L2 regularization. To control overfitting, the regularization term lambda was set to 1e−6.

The limited memory Broyden-Fletcher-Goldfarb-Shanno quasi-Newton algorithm (LBFGS) was employed to minimize the loss function. Although the model’s performance on the hold-out test dataset varied slightly with different random seed initializations, the model performance on the out-of-distribution live dataset varied greatly. The training was rerun using the same model architecture and data, but with a varied random seed (while keeping the random number generator to default: ‘twister’). The model that performed best on the live test dataset with a random seed value of 94202 (random number generator initialized with seed-1 in our code) was ultimately selected.

The loss curve for the model is shown in Supplementary Fig. 15b, where the training is terminated at the 66th epoch. The final selected model (at epoch = 45) has minimum validation loss indicated by the green vertical line.

To determine feature importance, we conducted the Shapley additive explanations (SHAP) test in Python 3.9.7 using SHAP API. The MATLAB model parameters were exported to Python to use the SHAP Python API.

IBM architecture and training details

The IBM architecture is shown in Supplementary Fig. 15c. It was specified as a standard Efficient Net B7 architecture with pretrained weights downloaded from the Pytorch-torchvision models package. The classification head was replaced with a 3-layer classifier of shape [2560, 500, 200] with two classes as output and the dropout rate in the classifier was changed from the default 0.5 to 0.3. The model requires the inputs to be in shape [633, 600]; hence, images were downscaled from 1280 × 1280 to 633 × 600. Random horizontal flips (p = 0.8), random vertical flips (p = 0.7), and random rotations from −30 to +30 degrees were used to augment the training data. Augmentation was performed using the torchvision transforms. The input images to the model were three-channel images called z-slices, with each channel being a neighboring z-section to the central image. The 3-channel image was normalized between the minimum and maximum value of the entire 3-channel stack.

All the model layers except the last convolutional layer (layer 8.0) and the subsequent classifier head were fixed for training. The model was trained using the standard cross-entropy loss with a learning rate of 5e−6. In addition, we employed exponential learning rate decay with a gamma value of 0.9. The standard Adam optimizer with all default parameters except the learning rate was used for loss optimization. The training batch size was set to 4 with a validation batch size of 1. The model was trained on 3809 images (52 embryos) and validated on 1297 images (21 embryos). The remaining images (79 embryos) were kept as a holdout for testing to be combined with data from other subsequent experiments (43 embryos) to create a test set randomized over the multiple cycles of experiments. The loss curve for the model training is shown in Supplementary Fig. 15d. The loss converged, and the model training was stopped after 100 epochs after no major improvements in the loss were observed.

We employed Grad-CAM^52,53 to detect decisive features in the image. The Grad-CAM maps were extracted after the last convolutional layer of the Efficient-Net B7. The model and associated codes were developed in Python 3.9.7 and Pytorch 1.11.0 and trained on NVIDIA GeForce RTX 3060 Ti. The training for 100 epochs took ~48 h.

Max-voting procedure

For both the FBM and the IBM, max-voting of individual nuclei/z-slice image predictions was performed to get the overall embryo-level predictions, meaning that the class which was predicted the most for the overall embryo was selected as the final class. Confidence probability was then the average of prediction scores over the majority class subset of nuclei/z-slice image for FBM, IBM respectively.

Automation of workflow using the MATLAB app

All the MATLAB-based processing codes were combined to develop a MATLAB app to demonstrate EVATOM (Supplementary Movie M4). The app has three panels. The first is to decide the segmentation parameters for initial 2D and final 3D segmentation based on nuclei predictions, as shown in Supplementary Fig. 16. After segmentation, the second panel (Supplementary Fig. 17) analyzes features and performs health grading. The third panel (Supplementary Fig. 18) is for demonstrating sparse predictions on a random set of z-slices. The detailed protocol is discussed in the Supplementary Note 2: MATLAB app operation.

ROC fitting and standard error estimation

The ROC curves in Supplementary Fig. 7 were fitted to extract standard error of the mean (sem) values using the ROC analysis tool developed by Metz et al.⁶⁴. We chose semi-parametric estimation with a conventional binormal ROC curve model. The inverse of the information matrix was selected as the uncertainty estimation method.

Statistics and reproducibility

All the extracted features were first tested for normality using Lilliefors Test (at 5% significance). All the features except nucleus count and bw3dB were found to be non-normal (Supplementary Table 1). Kruskal Wallis non-parametric test (at 0.1% significance) was applied to test for differences in the distribution between the three classes: healthy (H), intermediate (I), and sick (S). Post-hoc Dunn-multiple comparison test with Holm p-value adjustment was applied to determine the pairwise differences in the distribution (Supplementary Table 1). The nucleus count and bw3dB were normally distributed thus the Levene test was applied to test for equality of variance. The variances were similar (p > 0.001, the null hypothesis was not rejected). We then applied one-way ANOVA and Student T-test post-hoc test with Holm adjustment to test for deviations in group means. Results are shown in Supplementary Table 1. Comparisons between dry mass density of ICM and TE nuclei were performed for independent testing of three classes: healthy, intermediate, and sick (Fig. 4b) and two classes: blastocyst and cleavage-stage (Fig. 4c). Statistical significance of the difference between ICM and TE nuclei for each category was tested by performing Kruskal Wallis non-parametric test (at 0.01% significance). Figure legends and Supplementary Table 1 specify the sample size for each statistical test.

All the statistical analysis was performed in Python 3.9.7. In addition, we used the following libraries for individual tests: Lilliefors (statsmodel api), Kruskal-Wallis test, Levene test, one-way ANOVA test (scipy stats), Dunn’s posthoc, post-hoc Student T test (scikit posthoc).

Reproducibility is ensured through model testing on data collected over multiple rounds (n > 2) of sample preparation and imaging experiments while also incorporating different sample conditions (fixed and live embryos).

3D renderings

Amira (Thermo Fisher Scientific) was used for the renderings shown in Fig. 2d, e, and Supplementary movie M2. Clear volume (Fiji, ImageJ, NIH) was used for Fig. 2f. MATLAB 2022b (MathWorks) was used for all other 3D renderings.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.